函数乘法公式怎么输入
2025-03-11 09:10来源:网络本地 92人已围观
摘要明白了,下面是按照函数乘法公式怎么输入写的文章: 探索函数乘法公式:原理、应用与实践技巧 在数学的广阔领域中,函数是构建复杂数学模型和解决...

明白了,下面是按照函数乘法公式怎么输入写的文章:
探索函数乘法公式:原理、应用与实践技巧
在数学的广阔领域中,函数是构建复杂数学模型和解决问题的关键工具。而函数乘法作为基础运算之一,其基本原理和应用方法同样重要。本文将为您详细介绍函数乘法公式的相关知识,帮助您更好地理解和运用这一重要概念。
1. 函数乘法的基本概念
我们需要明确函数乘法的定义。函数乘法通常指的是两个或多个函数在同一变量取值下相乘的结果。这种运算形式在数学中具有广泛的应用,特别是在解决涉及多个变量的问题时。
例如,假设我们有两个函数 \( f(x) = x^2 \) 和 \( g(x) = 3x + 2 \),它们的乘积可以表示为:
\[ (f(x) g(x)) = (x^2) (3x + 2) = 3x^3 + 2x^2 + 6x + 2 \]
这个例子展示了如何通过函数乘法将两个函数的结果进行组合,从而得到一个新的函数表达式。
2. 函数乘法的性质
函数乘法也遵循一些基本的数学性质,这些性质对于理解函数乘法的应用至关重要。
- 交换律:对于任意两个函数 \( f(x) \) 和 \( g(x) \),都有 \( f(g(x)) = g(f(x)) \)。这意味着无论哪个变量在前,两个函数相乘的结果都是相同的。
- 结合律:对于任意三个函数 \( f(x) \)、\( g(x) \) 和 \( h(x) \),有 \( (f(g(x)) h(x)) = f(g(x)) h(x) \)。这表示三个函数相乘的顺序不影响结果。
- 分配律:对于任意两个函数 \( f(x) \) 和 \( g(x) \),有 \( f(g(x)) h(x) = f(g(x)) h(g(x)) \)。这意味着两个函数相乘的结果再与第三个函数相乘,其顺序不会影响最终结果。
这些性质不仅帮助我们更好地理解和计算函数乘法的结果,还为解决实际问题提供了有力的工具。
3. 函数乘法的应用
函数乘法的应用非常广泛,涵盖了从理论到实践的各个层面。以下是一些常见的应用领域实例:
- 经济学:在经济学中,函数乘法常用于分析不同经济变量之间的关系,如收入、消费和储蓄之间的乘积关系。通过研究这些乘积关系,可以揭示经济活动的内在规律。
- 物理学:在物理学中,函数乘法用于描述各种物理现象之间的相互作用。例如,牛顿第二定律中的力与加速度的乘积关系,以及电磁学中的电场强度与磁场强度的乘积关系。
- 计算机科学:在计算机科学中,函数乘法用于处理复杂的数据结构和算法。例如,哈希表的查找过程就是一个典型的函数乘法应用,其中键与值的乘积决定了哈希表中的位置。
- 统计学:在统计学中,函数乘法用于构建统计模型和进行数据分析。例如,回归分析中的线性回归模型就是通过两个变量的乘积来拟合数据点的过程。
4. 函数乘法的计算技巧
虽然函数乘法的概念简单直观,但在实际应用中,计算过程可能相对复杂。以下是一些实用的计算技巧,可以帮助您更高效地完成函数乘法的计算:
- 分解因式:当遇到难以直接计算的函数乘法表达式时,可以尝试将其分解为更简单的因式乘积形式。例如,\( a^2 + b^2 = (a + b)(a - b) \)。
- 使用计算器:现代计算器通常具备强大的数值计算功能,可以快速计算大多数函数乘法表达式的结果。在需要精确计算的情况下,使用计算器是一个便捷而有效的选择。
- 编程辅助:对于复杂的函数乘法问题,可以使用编程语言(如Python、R等)进行自动化计算。借助编程工具的强大功能,可以快速处理大量的函数乘法表达式,并生成所需的结果。
5. 结语
函数乘法作为数学中的一个基本运算,其原理和应用方法同样重要。通过深入理解函数乘法的基本概念、性质和应用技巧,我们可以更好地掌握这一重要工具。无论是在学术研究还是实际生活中,函数乘法都扮演着不可或缺的角色。让我们携手共进,不断探索和深化对函数乘法的理解,以应对日益复杂的数学问题和挑战。
Tags:
上一篇:模拟人生4怎么搬家
下一篇:没有了
相关文章
随便看看
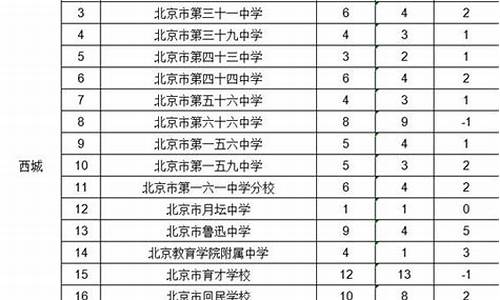
西城区高中排名
好的,以下是根据您的需求生成的文章: 西城区作为北京市的核心区域之一,...
论文怎么引用文献如何标注(论文引用文献
好的,以下是按照论文怎么引用文献如何标注写的文章: 论文写作中如何正确...
答辩不会的问题怎么回答(答辩时不会的问
明白,以下是根据您的要求生成的文章内容: 答辩不会的问题怎么回答 在参加...
红印子怎么快速去掉(红印子怎么快速去掉
好的,我将按照您的要求生成一篇关于红印子怎么快速去掉的文章: 如何迅速...
陌陌怎么问约不约
好的,按照您的要求生成了一篇1600字左右的文章: 掌握沟通的艺术:如何用陌...
小妙招塑料老化粘手怎么去除
明白,您需要一篇关于小妙招塑料老化粘手怎么去除的文章。以下是根据您要求...
被下迷糊药怎么症状
警惕迷糊药的副作用 在现代社会,由于生活节奏加快和工作压力增大,越来越...
五孔开关插座怎么接线(五孔开关插座怎么
五孔开关插座是一种常见的电器配件,通常用于家庭和办公室等场所。它由一个...






